How Big is The World?

Now, it may be obvious to most that we already know how big the surface area of the  world is. You may not know the exact number, but a simple Google search can tell you all you need: 197 million square miles, of which only 29% is land.  But how did we get there? Certainly, someone did not use a measuring tape around all the  continents and land masses of the world. The puzzle of how big the world is was solved both implicitly and explicitly by mathematicians!  

The first step towards finding out how big the world is started with the Greek mathematician  Pythagoras (or, rather, it started with the Babylonians some thousand years earlier, but that is  a debate we will not discuss). c.540 BC was when he created what we know today as Pythagoras’ theorem. This theorem stated that in a right-angle triangle, the square of the length of  the longest side was equal to the sum of the  squares of the two shorter sides. This is seen in the figure included.

Pythagoras’ theorem, although formulated  circa 540 BC, was proved by Euclid of  Alexandria some 300 years later. It then developed  into trigonometry, where we could find the lengths  of a right-angled triangle using one length,  and two angles, rather than two whole lengths. Trigonometry saved time in physical applications and lengthy calculations.  

But how does this relate to the measurement of the world?  

Well, it doesn’t. Not yet. Pythagoras’ theorem was used successfully for early maps of the  world, but before I explain the how, it is important that we acknowledge the earliest and most  accurate map that did not use the theorem. 

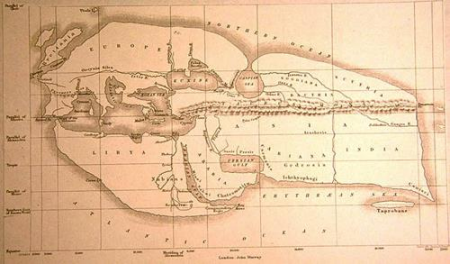
The map shown was not drawn by a modern American. In fact, it was drawn by  Eratosthenes, yet another Greek polymath, based in modern day Libya. He was born around  267 BC – later than Pythagoras. His method to measure the Earth was different to the way we  have done it today. He observed that at noon on the longest day of the year the sun’s rays fell  on the Earth at different angles in different places. But he discovered that the angle between  the sun’s rays and objects perpendicular to the Earth’s surface was almost zero.

So,  to investigate this, he placed a vertical stick of a known height in two cities, on the same day, and measured the length of a shadow it created. A combination of the north-south distance between the two cities and the angles measured gave a ratio which allowed Eratosthenes to calculate the size of the Earth. This, of course, is a simplified version of events, but is its essence. Despite the contemporary ignorance of the continents of Asia and Africa, (the other hemisphere), he still managed to map the size of  the world pretty accurately (to be precise, within  2% of the modern measured value). There are some debates as to whether Eratosthenes  discovered this himself, or whether this way of   measurement was an accepted way of life in his  time. Nonetheless, the method is impressive. He was able to deduce the size of the earth. Comparing it against the supposed size of the Earth that had been established through word of mouth and celestial observations, he was also able to understand the amount of Earth unknown to him. Considering the lack of satellite technology and knowledge of the hemisphere, the measurement of the size of Earth is impressively accurate.  

Another more accurate answer to the question, ‘how big is the Earth?’, was presented by  Willebrord Snellius in the early 17th century, a Dutch mathematician. What was his method if not Eratosthenes’ method? Snellius used triangulation. This is where an area is  surveyed by a network of triangles. He was able to put to work the theorem of Pythagoras,  and the subsequently developed ideas of trigonometry. Snellius begun   by working out the distance between two Dutch towns, Alkmaar and Bergen op Zoom, using a network of 33 triangles. These towns lay on the  same longitude and were exactly one degree of arc apart, thus   assumptions that they lay on a flat plane could be made. This means he,  unlike Eratosthenes, could use just one length and two angles, rather than two lengths and multiple angles, much more efficient! He would find, using one length and two angles, another two lengths, which would, in turn, become the lengths to use for another triangle, and so on. After accurately measuring the distance between these towns, he  went on to measure the world. The same trigonometry could pinpoint exact locations of important landmarks like churches, crossroads, schools etc. It was used in the late 18th century in the Great Trigonometric Survey of India, which mapped the Himalayas and determined the height of Mount Everest. This is a method still used today in  technology and is also used in architecture. Triangulation can be seen in the architecture of the Golden Gate Bridge in San Francisco, as well as the Eiffel Tower in Paris.  

The most accurate and most modern answer to the question is given by satellite technology. But that does not mean we cannot give credit where credit is due; triangles mapped the  world! Although explicit triangulation is no longer used, it is still here in the methods used to  deduce locations from satellite data, and it did, in fact, answer the question: How big is the  world? 

---

Written by Hannah Hamid 

References

• Calculating the Size of Earth | Brilliant Math & Science Wiki

• Triangulation (surveying) - Wikipedia 

• Spherical Earth - Wikipedia 

• 17 Equations That Changed the World by Ian Stewart - PII: 0315-0860(84)90025-9 (sciencedirectassets.com) - 5.4: Measuring the Earth with Eratosthenes - Physics LibreTexts